
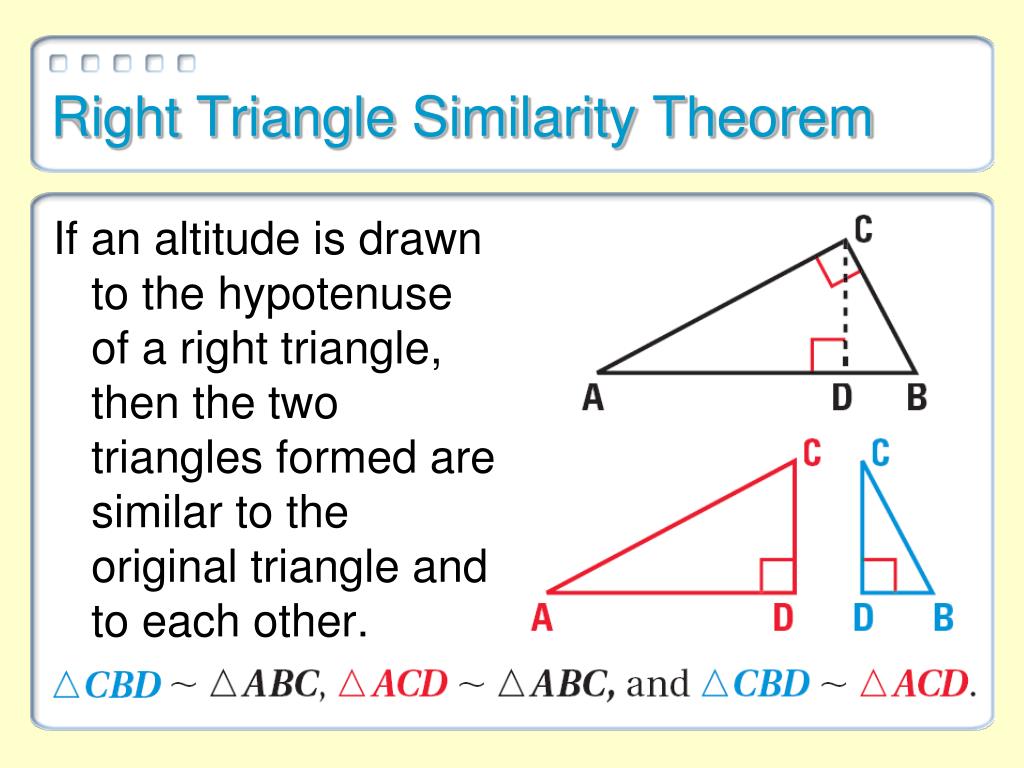
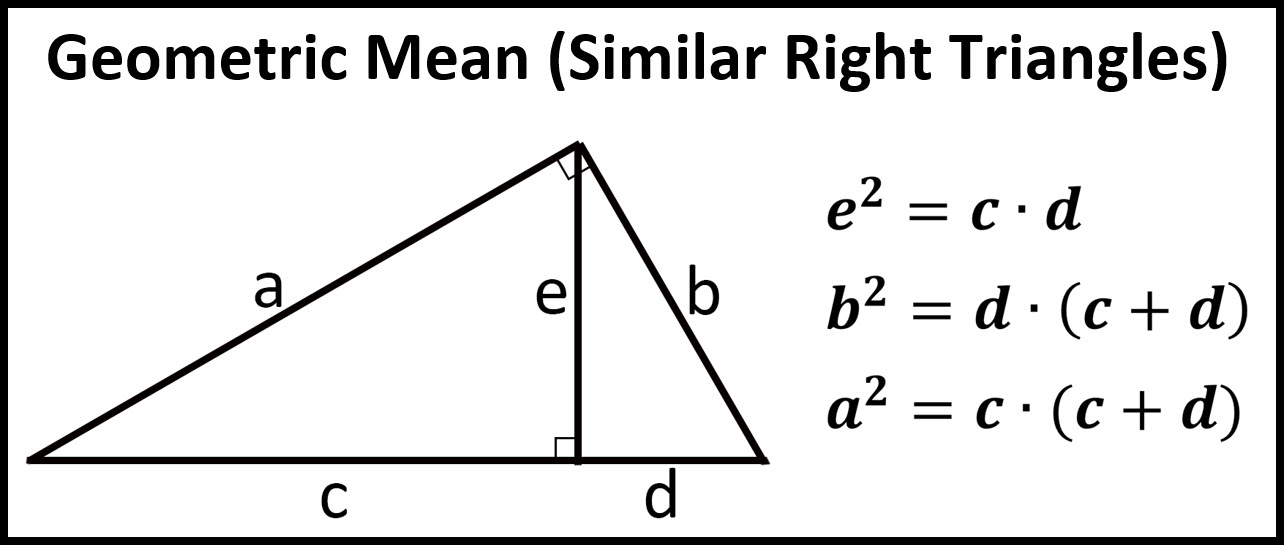
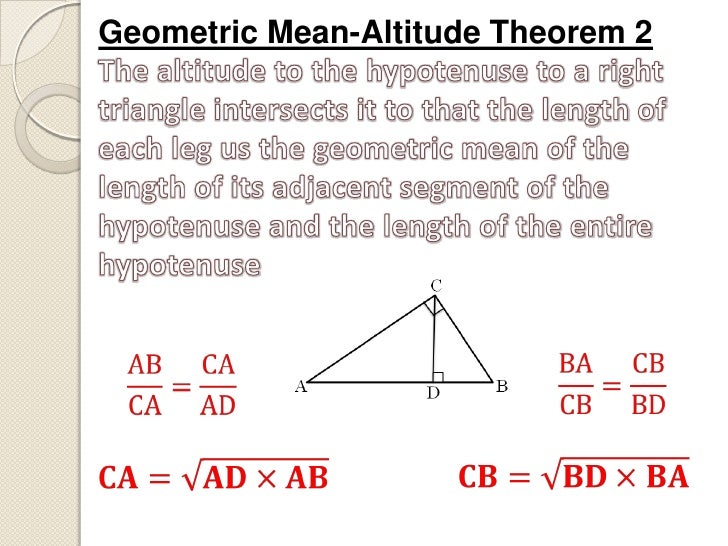
Check it out!!! A surveyor positions himself so that his line of sight to the top of a cliff and his line of sight to the bottom form a right angle as shown.What is the height of the tree to the nearest meter? The tree is about 38 + 1.6 = 39.6, or 40 m tall Her eyes are about 1.6 m above the ground, and she is standing 7.8 m from the tree. Example 4: Measurement Application To estimate the height of a Douglas fir, Jan positions herself so that her lines of sight to the top and bottom of the tree form a 90 angle.Check It Out! Example 3 Find u, v, and w.Example Example 3: Finding Side Lengths in Right Triangles Find x, y, and z.All the relationships in red involve geometric means. Similarity in right triangles You can use Theorem 8-1-1 to write proportions comparing the side lengths of the triangles formed by the altitude to the hypotenuse of a right triangle.If necessary, give the answer in simplest radical form. Check it out!! Find the geometric mean of each pair of numbers.Example Find the geometric mean of each pair of numbers.4 and 25 Solution Let x be the geometric mean. Example 2A: Finding Geometric Means Find the geometric mean of each pair of numbers.So the geometric mean of a and b is the positive number x such that, or x 2 = ab. The geometric mean of two positive numbers is the positive square root of their product. In this case, the means of the proportion are the same number, and that number is the geometric mean of the extremes. Geometric mean Consider the proportion.Check it out Write a similarity statement comparing the three triangles By Theorem 8-1-1, LJK ~ JMK ~ LMJ. .SRT.A.2 Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.Solution Sketch the three right triangles with the angles of the triangles in corresponding positions.Example #1 Write a similarity statement comparing the three triangles.Similarity in right triangles In a right triangle, an altitude drawn from the vertex of the right angle to the hypotenuse forms two right triangles.Apply similarity relationships in right triangles to solve problems. Objectives Use geometric mean to find segment lengths in right triangles.Chapter 8 8-1 Similarity in right triangles.
solve problems that involve triangle similarity and right triangles.
The module is comprised of only one lesson: But the order in which you read them can be changed to correspond with the textbook you are now using. The lessons are arranged to follow the standard sequence of the course. The language used recognizes the diverse vocabulary level of students. The scope of this module permits it to be used in many different learning situations. You will analyze and solve problems involving these concepts in real life situations. In this module, you will apply what you have learned about concepts and theorems in triangle similarity and right triangles. And read the instructions carefully before performing each task. Use a separate sheet of paper in answering the exercises and tests. Do not put unnecessary marks on any part of this SLM. Use geometric mean to find segment lengths in right triangles. We trust that you will be honest in using these. Answer keys are provided for each activity and test. At the end of each module, you need to answer the post-test to self-check your learning. This will tell you if you need to proceed on completing this module or if you need to ask your facilitator or your teacher’s assistance for better understanding of the lesson. Pre-tests are provided to measure your prior knowledge on lessons in each SLM. Each part shall guide you step-by-step as you discover and understand the lesson prepared for you. Activities, questions, directions, exercises, and discussions are carefully stated for you to understand each lesson.Įach SLM is composed of different parts. This Self-Learning Module (SLM) is prepared so that you, our dear learners, can continue your studies and learn while at home. To find the geometric mean of two numbers, just find the product of those numbers and take the square root Follow along with this tutorial to learn the process.


 0 kommentar(er)
0 kommentar(er)
